number theory is one of those areas in the mathematics , which develop a similar lure like the sirens in Greek mythology. Who dares go near it, it will be quickly enchanted by its beguiling simplicity. Many number theoretic problems seem incredibly simple, as you would have to sit down for just a short time with pen and paper, and the thing would be carved. But anyone who thinks so is already lost. So many naive victims has drawn the theory of numbers already cold with its brutal complexity to Ruin.
Only sometimes a mathematician victory but rich out of this fight. As recently Andrew Booker from the University of Bristol. He has ventured to a variant of the so-called diophant's equations, and a mathematician in ancient Greece are desperate. In the case of coverage Problem deals specifically with the question of which integers as a sum of three powers of other integers expressions. A simple example is the number 29 is: you can write as 33+13+13. For what other Numbers there are to pay triple? And how many of them?
8'866 128'975 287'5283 + (?8'778 405'442 862'239)3 + (?2'736 111'468 807'040)3 = 33
This can't be so hard, you might think, although one should bear in mind that negative Numbers are allowed. In fact, the Problem is intractable. For two groups of numbers, we know that no solutions exist: those Numbers, the Rest 4 or 5 through 9 parts, so 4, 5, 13, 14, 22, 23, 31, 32 and so on. Then again, there are Numbers, for the even a whole bunch of solutions is known. Since mathematicians 1954 began, the Problem with computers address, could be sorted in many Numbers in this group.
The most interesting but the problem cases are: Pay, for, in spite of an intensive search, no solution has yet been found, without, you know, however, why this is so. In numbers up to 1000, the long was 14 Figures. The list starts with 33, 42, 74, 114, 165, 390 and 579. At least that was the state in 2015, as the video-journalist Brady Haran, posted in his popular Youtube channel "Numberphile" Video, in which the British mathematician Tim Browning explained the Problem.
Haran knows the siren-like attraction of the subject, that's why the Video is provided, in its wisdom, with warnings: "don't stop to try it for yourself!" – in the case of the number 30, where the first solution only works with ten-digit Numbers. Or "Here, certainly not pause to try it for yourself": in the 33 for example, for which there was no solution.
The mathematician Andrew Booker left of this note, however, was not deterred when he saw the Video. At the first try, he was not far. But then he was on a second Numberphile Video that was released Haran 2016 – on the occasion of the first solution for the number 74. "As it has gripped me," said Booker in a third, the latest Video in the series. He took the remaining Numbers.
have Already tried many mathematicians to prove that for these Numbers, no solution exists, without success. Others have expected computers away, also without success. Booker fell, what could be the problem: All of the remaining 13 Numbers below 1000 are with a Rest of 3 or 6 divisible by 9. The could mean: While there are with their Relatives, the Rest 4 or 5 through 9 parts, not a single solution, have Numbers of this group, although an infinite number of solutions. But these are in the endless Expanses of the pay period, extremely rare and hard to find. It is, therefore, the scope of the search so far to narrow down the task for a Supercomputer is solvable.
Faster-than-expected to find it
And that is exactly what became Booker has succeeded, at least for the smallest number on the list: With a little Algebra, he was able to reshape the diophant of equation for the number 33 so that he could search with the computational cluster of his University specifically to find solutions to the billiard area. And there he was looking for, much faster than expected. After a few days of his program pending a solution. As Booker nachrechnete showed you was correct. 8'866 128'975 287'5283 + (?8'778 405'442 862'239)3 + (?2'736 111'468 807'040)3 is actually the 33. (Who would like to stop here to try it for yourself, you should use a program such as Wolfram Mathematica, with so many decimal places.)
What is missing is a proof of the conjecture, that for all the Numbers except for the remaining 4 or 5 by 9 divisible an infinite number of solutions. "Some people believe that this is undecidable," says Booker. "Maybe we will never have proof, and the closer we can come to the thing." Where: the 42 would be Yes. (Editorial Tamedia)
Created: 21.03.2019, 09:13 PM

 Sabadell rejects the merger with BBVA and will fight to remain alone
Sabadell rejects the merger with BBVA and will fight to remain alone In Germany, the far left wants to cap the price of “doner kebabs”
In Germany, the far left wants to cap the price of “doner kebabs” Israel-Hamas war: Gaza between hope of truce and fear of Israeli offensive in the South
Israel-Hamas war: Gaza between hope of truce and fear of Israeli offensive in the South “Mom, Dad, please don’t die”: in the United States, a nine-year-old child saves the lives of his parents injured in a tornado
“Mom, Dad, please don’t die”: in the United States, a nine-year-old child saves the lives of his parents injured in a tornado The presence of blood in the urine, a warning sign of bladder cancer
The presence of blood in the urine, a warning sign of bladder cancer A baby whose mother smoked during pregnancy will age more quickly
A baby whose mother smoked during pregnancy will age more quickly The euro zone economy grows in April at its best pace in almost a year but inflationary pressure increases
The euro zone economy grows in April at its best pace in almost a year but inflationary pressure increases Children born thanks to PMA do not have more cancers than others
Children born thanks to PMA do not have more cancers than others “House of the Dragon”, “Succession”… Max, the new streaming platform from HBO and Discovery, launched in France on June 11
“House of the Dragon”, “Succession”… Max, the new streaming platform from HBO and Discovery, launched in France on June 11 The A13 motorway will finally reopen this Friday, in one direction only
The A13 motorway will finally reopen this Friday, in one direction only TNT commission of inquiry: tensions between LFI deputies and Macronists before the vote on the report
TNT commission of inquiry: tensions between LFI deputies and Macronists before the vote on the report Apple unveils a new, more efficient iPad range
Apple unveils a new, more efficient iPad range The Gaza War invites itself to the 2024 Pulitzer Prizes
The Gaza War invites itself to the 2024 Pulitzer Prizes Judith Godrèche presents a short film on sexual violence in Cannes
Judith Godrèche presents a short film on sexual violence in Cannes Kevin Spacey: new trial in sight in London for the American actor, for sexual assault
Kevin Spacey: new trial in sight in London for the American actor, for sexual assault Taylor Swift fans make London pub Black Dog their new place of pilgrimage
Taylor Swift fans make London pub Black Dog their new place of pilgrimage Omoda 7, another Chinese car that could be manufactured in Spain
Omoda 7, another Chinese car that could be manufactured in Spain BYD chooses CA Auto Bank as financial partner in Spain
BYD chooses CA Auto Bank as financial partner in Spain Tesla and Baidu sign key agreement to boost development of autonomous driving
Tesla and Baidu sign key agreement to boost development of autonomous driving Skoda Kodiaq 2024: a 'beast' plug-in hybrid SUV
Skoda Kodiaq 2024: a 'beast' plug-in hybrid SUV The home mortgage firm rises 3.8% in February and the average interest moderates to 3.33%
The home mortgage firm rises 3.8% in February and the average interest moderates to 3.33% This is how housing prices have changed in Spain in the last decade
This is how housing prices have changed in Spain in the last decade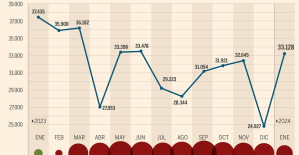 The home mortgage firm drops 10% in January and interest soars to 3.46%
The home mortgage firm drops 10% in January and interest soars to 3.46% The jewel of the Rocío de Nagüeles urbanization: a dream villa in Marbella
The jewel of the Rocío de Nagüeles urbanization: a dream villa in Marbella Institutions: senators want to restore the accumulation of mandates and put an end to the automatic presence of ex-presidents on the Constitutional Council
Institutions: senators want to restore the accumulation of mandates and put an end to the automatic presence of ex-presidents on the Constitutional Council Europeans: David Lisnard expresses his “essential and vital” support for François-Xavier Bellamy
Europeans: David Lisnard expresses his “essential and vital” support for François-Xavier Bellamy Facing Jordan Bardella, the popularity match turns to Gabriel Attal’s advantage
Facing Jordan Bardella, the popularity match turns to Gabriel Attal’s advantage Europeans: a senior official on the National Rally list
Europeans: a senior official on the National Rally list These French cities that will boycott the World Cup in Qatar
These French cities that will boycott the World Cup in Qatar “The future is for us”: “disappointed” and “proud” at the same time, Al-Khelaïfi sees the glass half full after the elimination of PSG
“The future is for us”: “disappointed” and “proud” at the same time, Al-Khelaïfi sees the glass half full after the elimination of PSG PSG: “Since January, these have not been my best matches,” agrees Zaire-Emery, who promises to “come back stronger”
PSG: “Since January, these have not been my best matches,” agrees Zaire-Emery, who promises to “come back stronger” “What is this question, honestly?” : Nasser Al-Khelaïfi (very) annoyed after PSG-Dortmund
“What is this question, honestly?” : Nasser Al-Khelaïfi (very) annoyed after PSG-Dortmund “I am the guy who has to score the goals”: Mbappé does not hide and assumes responsibility after PSG’s exit
“I am the guy who has to score the goals”: Mbappé does not hide and assumes responsibility after PSG’s exit