number theory is one of those areas in the mathematics , which develop a similar lure like the sirens in Greek mythology. Who dares go near it, it will be quickly enchanted by its beguiling simplicity. Many number theoretic problems seem incredibly simple, as you would have to sit down for just a short time with pen and paper, and the thing would be carved. But anyone who thinks so is already lost. So many naive victims has drawn the theory of numbers already cold with its brutal complexity to Ruin.
Only sometimes a mathematician victory but rich out of this fight. As recently Andrew Booker from the University of Bristol. He has ventured to a variant of the so-called diophant's equations, and a mathematician in ancient Greece are desperate. In the case of coverage Problem deals specifically with the question of which integers as a sum of three powers of other integers expressions. A simple example is the number 29 is: you can write as 33+13+13. For what other Numbers there are to pay triple? And how many of them?
8'866 128'975 287'5283 + (?8'778 405'442 862'239)3 + (?2'736 111'468 807'040)3 = 33
This can't be so hard, you might think, although one should bear in mind that negative Numbers are allowed. In fact, the Problem is intractable. For two groups of numbers, we know that no solutions exist: those Numbers, the Rest 4 or 5 through 9 parts, so 4, 5, 13, 14, 22, 23, 31, 32 and so on. Then again, there are Numbers, for the even a whole bunch of solutions is known. Since mathematicians 1954 began, the Problem with computers address, could be sorted in many Numbers in this group.
The most interesting but the problem cases are: Pay, for, in spite of an intensive search, no solution has yet been found, without, you know, however, why this is so. In numbers up to 1000, the long was 14 Figures. The list starts with 33, 42, 74, 114, 165, 390 and 579. At least that was the state in 2015, as the video-journalist Brady Haran, posted in his popular Youtube channel "Numberphile" Video, in which the British mathematician Tim Browning explained the Problem.
Haran knows the siren-like attraction of the subject, that's why the Video is provided, in its wisdom, with warnings: "don't stop to try it for yourself!" – in the case of the number 30, where the first solution only works with ten-digit Numbers. Or "Here, certainly not pause to try it for yourself": in the 33 for example, for which there was no solution.
The mathematician Andrew Booker left of this note, however, was not deterred when he saw the Video. At the first try, he was not far. But then he was on a second Numberphile Video that was released Haran 2016 – on the occasion of the first solution for the number 74. "As it has gripped me," said Booker in a third, the latest Video in the series. He took the remaining Numbers.
have Already tried many mathematicians to prove that for these Numbers, no solution exists, without success. Others have expected computers away, also without success. Booker fell, what could be the problem: All of the remaining 13 Numbers below 1000 are with a Rest of 3 or 6 divisible by 9. The could mean: While there are with their Relatives, the Rest 4 or 5 through 9 parts, not a single solution, have Numbers of this group, although an infinite number of solutions. But these are in the endless Expanses of the pay period, extremely rare and hard to find. It is, therefore, the scope of the search so far to narrow down the task for a Supercomputer is solvable.
Faster-than-expected to find it
And that is exactly what became Booker has succeeded, at least for the smallest number on the list: With a little Algebra, he was able to reshape the diophant of equation for the number 33 so that he could search with the computational cluster of his University specifically to find solutions to the billiard area. And there he was looking for, much faster than expected. After a few days of his program pending a solution. As Booker nachrechnete showed you was correct. 8'866 128'975 287'5283 + (?8'778 405'442 862'239)3 + (?2'736 111'468 807'040)3 is actually the 33. (Who would like to stop here to try it for yourself, you should use a program such as Wolfram Mathematica, with so many decimal places.)
What is missing is a proof of the conjecture, that for all the Numbers except for the remaining 4 or 5 by 9 divisible an infinite number of solutions. "Some people believe that this is undecidable," says Booker. "Maybe we will never have proof, and the closer we can come to the thing." Where: the 42 would be Yes. (Editorial Tamedia)
Created: 21.03.2019, 09:13 PM

 United States: divided on the question of presidential immunity, the Supreme Court offers respite to Trump
United States: divided on the question of presidential immunity, the Supreme Court offers respite to Trump Maurizio Molinari: “the Scurati affair, a European injury”
Maurizio Molinari: “the Scurati affair, a European injury” Hamas-Israel war: US begins construction of pier in Gaza
Hamas-Israel war: US begins construction of pier in Gaza Israel prepares to attack Rafah
Israel prepares to attack Rafah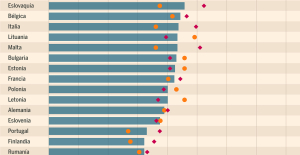 Spain is the country in the European Union with the most overqualified workers for their jobs
Spain is the country in the European Union with the most overqualified workers for their jobs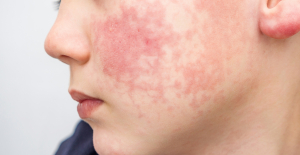 Parvovirus alert, the “fifth disease” of children which has already caused the death of five babies in 2024
Parvovirus alert, the “fifth disease” of children which has already caused the death of five babies in 2024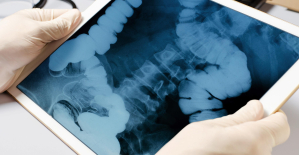 Colorectal cancer: what to watch out for in those under 50
Colorectal cancer: what to watch out for in those under 50 H5N1 virus: traces detected in pasteurized milk in the United States
H5N1 virus: traces detected in pasteurized milk in the United States Private clinics announce a strike with “total suspension” of their activities, including emergencies, from June 3 to 5
Private clinics announce a strike with “total suspension” of their activities, including emergencies, from June 3 to 5 The Lagardère group wants to accentuate “synergies” with Vivendi, its new owner
The Lagardère group wants to accentuate “synergies” with Vivendi, its new owner The iconic tennis video game “Top Spin” returns after 13 years of absence
The iconic tennis video game “Top Spin” returns after 13 years of absence Three Stellantis automobile factories shut down due to supplier strike
Three Stellantis automobile factories shut down due to supplier strike A pre-Roman necropolis discovered in Italy during archaeological excavations
A pre-Roman necropolis discovered in Italy during archaeological excavations Searches in Guadeloupe for an investigation into the memorial dedicated to the history of slavery
Searches in Guadeloupe for an investigation into the memorial dedicated to the history of slavery Aya Nakamura in Olympic form a few hours before the Flames ceremony
Aya Nakamura in Olympic form a few hours before the Flames ceremony Psychiatrist Raphaël Gaillard elected to the French Academy
Psychiatrist Raphaël Gaillard elected to the French Academy Skoda Kodiaq 2024: a 'beast' plug-in hybrid SUV
Skoda Kodiaq 2024: a 'beast' plug-in hybrid SUV Tesla launches a new Model Y with 600 km of autonomy at a "more accessible price"
Tesla launches a new Model Y with 600 km of autonomy at a "more accessible price" The 10 best-selling cars in March 2024 in Spain: sales fall due to Easter
The 10 best-selling cars in March 2024 in Spain: sales fall due to Easter A private jet company buys more than 100 flying cars
A private jet company buys more than 100 flying cars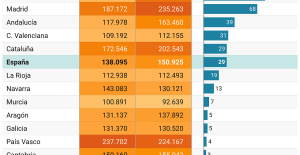 This is how housing prices have changed in Spain in the last decade
This is how housing prices have changed in Spain in the last decade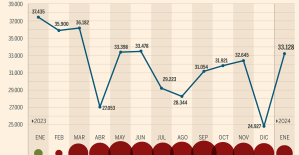 The home mortgage firm drops 10% in January and interest soars to 3.46%
The home mortgage firm drops 10% in January and interest soars to 3.46% The jewel of the Rocío de Nagüeles urbanization: a dream villa in Marbella
The jewel of the Rocío de Nagüeles urbanization: a dream villa in Marbella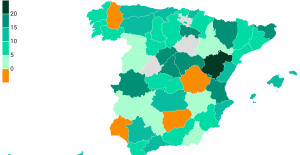 Rental prices grow by 7.3% in February: where does it go up and where does it go down?
Rental prices grow by 7.3% in February: where does it go up and where does it go down? Even on a mission for NATO, the Charles-de-Gaulle remains under French control, Lecornu responds to Mélenchon
Even on a mission for NATO, the Charles-de-Gaulle remains under French control, Lecornu responds to Mélenchon “Deadly Europe”, “economic decline”, immigration… What to remember from Emmanuel Macron’s speech at the Sorbonne
“Deadly Europe”, “economic decline”, immigration… What to remember from Emmanuel Macron’s speech at the Sorbonne Sale of Biogaran: The Republicans write to Emmanuel Macron
Sale of Biogaran: The Republicans write to Emmanuel Macron Europeans: “All those who claim that we don’t need Europe are liars”, criticizes Bayrou
Europeans: “All those who claim that we don’t need Europe are liars”, criticizes Bayrou These French cities that will boycott the World Cup in Qatar
These French cities that will boycott the World Cup in Qatar Archery: everything you need to know about the sport
Archery: everything you need to know about the sport Handball: “We collapsed”, regrets Nikola Karabatic after PSG-Barcelona
Handball: “We collapsed”, regrets Nikola Karabatic after PSG-Barcelona Tennis: smash, drop shot, slide... Nadal's best points for his return to Madrid (video)
Tennis: smash, drop shot, slide... Nadal's best points for his return to Madrid (video) Pro D2: Biarritz wins a significant success in Agen and takes another step towards maintaining
Pro D2: Biarritz wins a significant success in Agen and takes another step towards maintaining


















